La période de crise sanitaire actuelle est marquée par un regain d’intérêt pour l’analyse de données épidémiologiques. Elle a porté sur le devant de la scène médiatique certains concepts clés de l’expérimentation scientifique, telle la notion d’essai clinique. De façon liée, on a pu entendre de nombreux appels à la prudence dans l’interprétation de résultats issus d’études observationnelles – c’est-à-dire portant sur l’analyse de caractéristiques d’un groupe de patients et patientes sans aucune intervention particulière de la part des scientifiques (p.ex. l’administration d’un traitement particulier)¹. Je voudrais ici insister sur les limites inhérentes aux études observationnelles, en illustrant à quel point il est facile d’obtenir une corrélation fallacieuse entre deux pathologies (ou plus généralement deux conditions médicales) lorsque l’on s’intéresse à des données recueillies chez des personnes admises à l’hôpital.

On le sait, corrélation n’implique pas causalité, et il est donc extrêmement délicat de déterminer à partir de la simple observation d’une association statistique entre deux facteurs A et B si A entraîne B, si B entraîne A, si A entraîne indirectement B par le biais de X ou encore si A et B dépendent tous deux d’un troisième facteur C non mesuré (voir partie gauche de la figure 1). Il s’agit là d’explications liées à des mécanismes sous-jacents. Même si elles suggèrent que la recherche des causes premières peut s’avérer ardue, ces trois explications supposent néanmoins que A et B sont effectivement liés une relation réelle, directe ou non, et engagent donc à une étude plus approfondie. Le volet droit de la figure 1 liste deux explications liées non à la relation entre A et B mais aux conditions d’observation. Primo, le cas bien connu de la coïncidence malencontreuse : observer, par malchance, une corrélation entre A et B sur les données considérées, alors que les deux facteurs sont en réalité complètement indépendants (voir des exemples sur le site spurious correlation). Une solution simple dans ce cas consiste à réitérer la mesure sur un groupe de données distinct pour s’assurer de sa reproductibilité. Dans la suite de ce billet, je décrirai un cinquième cas de figure moins connu, bien que tout aussi fréquent et peut-être plus problématique, dans lequel une corrélation est observée de façon robuste entre deux facteurs totalement indépendants. Ce phénomène statistique est désigné sous plusieurs noms : contrôle pour un collisionneur (collider), distorsion-sélection, biais (ou paradoxe²) de Berkson [1], [2].

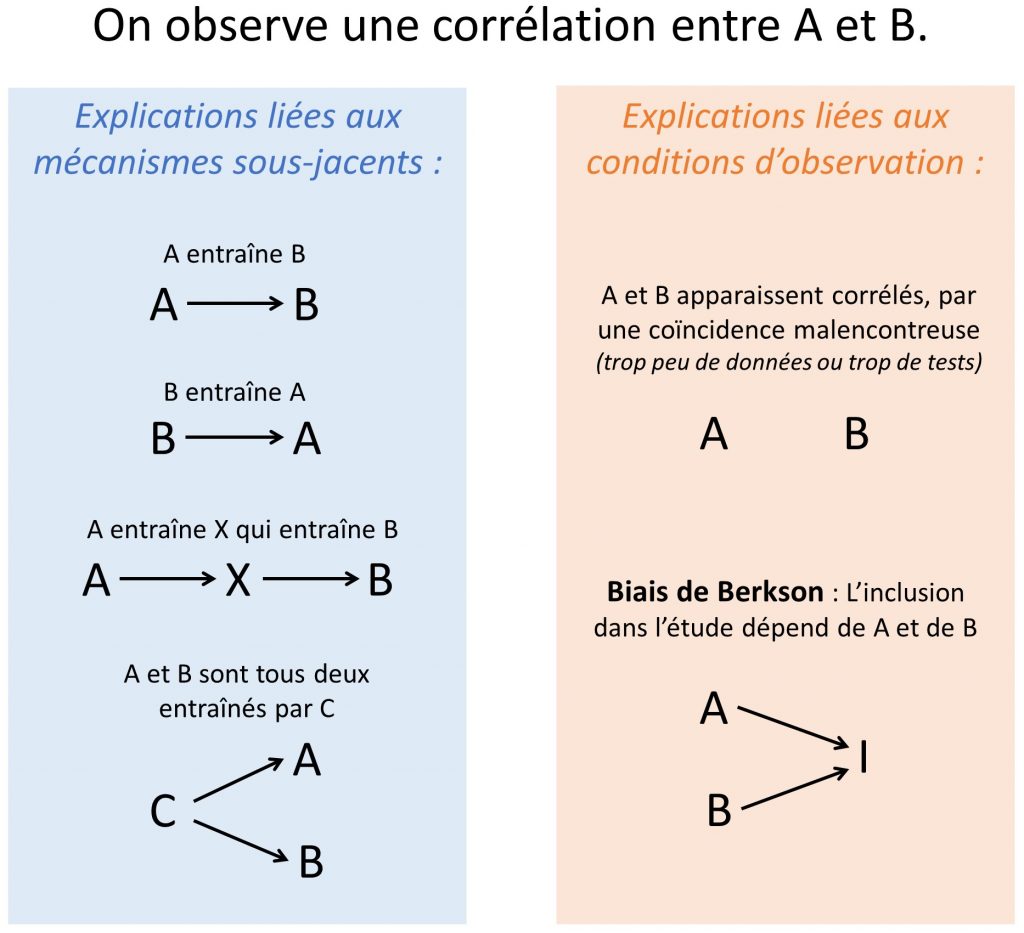
Figure 1. Six explications possibles (non exclusives) à l’observation d’une corrélation entre deux phénomènes ou deux variables A et B.

Imaginons deux pathologies parfaitement indépendantes dans les mécanismes qui les engendrent, mais se traduisant toutes les deux par une toux plus ou moins forte. Leur gravité est mesurée chez un individu par les variables A et B, respectivement. Voici une simulation de ce qu’on pourrait obtenir à l’échelle de la population totale, en représentant chaque individu par un cercle.

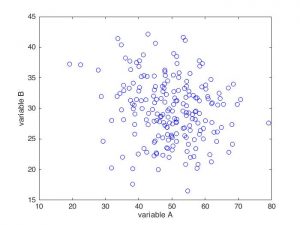
Les deux pathologies étant indépendantes, on n’observe pas de corrélation sur ce graphe : les points se répartissent en un nuage relativement homogène et isotrope. Autrement dit, connaître la valeur A pour un individu ne nous permet pas d’en déduire, même de façon approximative, sa valeur B, et inversement.

Au sein de cette population, un certain nombre de personnes vont ressentir des symptômes de toux inquiétants et se rendre à l’hôpital. La toux étant causée indifféremment par l’une ou l’autre pathologie, c’est chez les individus globalement situés dans le quart supérieur droit du graphique qu’elle se déclenchera (individus avec les plus grandes valeurs A et/ou B, représentés en rouge dans la figure ci-dessous).

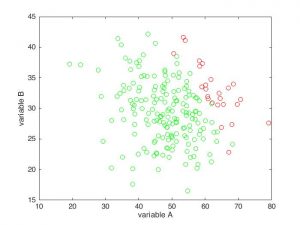
Supposons à présent que nous menions une étude observationnelle sur la pathologie A. Nous recueillons les données cliniques de l’ensemble des personnes qui se sont présentées à l’hôpital avec des symptômes de toux (les cercles rouges ci-dessus, reproduits dans la figure suivante) pour examiner, chez les individus malades, le lien éventuel entre la pathologie A et d’autres conditions médicales. Chez ces patientes et patients, nous observons une forte corrélation négative entre les deux pathologies, qui sont pourtant, rappelons-le, totalement indépendantes. Sans une vigilance particulière, nous pourrions donc être amenés à conclure à tort que les pathologies A et B interagissent d’une certaine manière, voire que A protègerait efficacement de B par un quelconque mécanisme biologique.

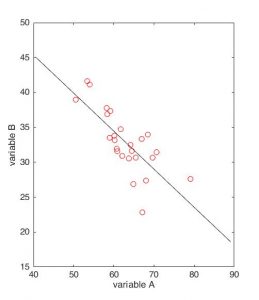
Cet exemple illustre un cas typique de biais de Berkson : la sélection des participants et participantes de l’étude (ici l’admission à l’hôpital), introduit une corrélation négative sur les critères d’inclusion. Pourquoi ? Parce que si un individu du groupe rouge a une valeur A basse, il a alors nécessairement une valeur B haute, sans quoi il n’aurait pas déclaré de symptôme de toux et n’aurait pas été comptabilisé dans l’étude. Inversement, s’il présente une valeur B basse, on peut en déduire logiquement que son score A est élevé puisque cette personne se trouve à l’hôpital. Il en résulte que, en moyenne, une valeur A élevée est plus souvent associée à une valeur B basse, et réciproquement, soit une corrélation négative entre A et B. Il s’agit donc d’une forme particulière de biais de sélection : la patientèle de l’hôpital utilisée comme échantillon de l’étude n’est ici pas représentative de la répartition des deux pathologies dans la population globale.

Le biais de Berkson peut se manifester dans les domaines les plus divers, même lorsque le processus de sélection n’est pas apparent. Pourquoi les joueurs de basketball les moins grands semblent-ils également les plus agiles ? Parce que les joueurs petits et maladroits ne sont tout simplement pas sélectionnés. Pourquoi les restaurants les mieux situés sont-ils généralement moins bons ? Parce que les restaurants mauvais et mal localisés ont déjà fait faillite. Pourquoi observe-t-on, chez les élèves entrant dans un cursus généraliste, une corrélation négative entre les notes scientifiques et littéraires ? Parce que les candidats et candidates qui ont obtenu des mauvaises notes à la fois dans les matières scientifiques et dans les matières littéraires n’ont pas été admis [2]. Pourquoi semble-t-il exister une relation négative entre la rigueur d’une publication scientifique et son caractère médiatique ? Parce que les travaux approximatifs et sans intérêt journalistique ne sont pas publiés³ [1]. Ceci engage donc à prêter une attention accrue aux processus aboutissant à la constitution de notre échantillon d’observation : si les critères d’inclusion dépendent directement ou indirectement des variables étudiées, ceux-ci peuvent distordre les relations observées entre ces variables, au point de faire apparaître artificiellement des corrélations entre des facteurs totalement indépendants. Même si je n’ai mentionné ici que l’exemple le plus simple, celui de la régression linéaire, le même phénomène statistique peut se produire au sein de modèles statistiques plus complexes. C’est souvent le cas lorsqu’un grand nombre de variables contrôle sont incluses « à l’aveugle » dans une régression multivariée (j’ai déjà mentionné cet écueil au paragraphe 2.1 d’un précédent billet)⁴.

Comme je l’ai évoqué en introduction (figure 1), le biais de Berkson n’est qu’une des explications possibles à l’observation d’une corrélation entre deux facteurs. Il est néanmoins particulièrement dangereux : un grand nombre d’études observationnelles sont réalisées sur une population hospitalière, ce qui nous place dans une situation de biais de sélection. Par ailleurs, contrairement à la « coïncidence malencontreuse », il ne s’agit pas ici d’un effet purement aléatoire qui se dissipera lorsque l’expérience sera répliquée, mais au contraire d’un phénomène statistique robuste. La meilleure option pour se prémunir du biais de Berkson reste donc de se fier en premier lieu à des essais cliniques plutôt qu’à des études observationnelles, lorsque c’est possible⁵.

Références

[1] R. McElreath, Statistical Rethinking : A Bayesian Course with R Examples. Boca Raton, UNITED STATES: Chapman and Hall/CRC, 2015.
[2] J. Pearl, Causality: Models, Reasoning, and Inference. Cambridge University Press, 2009.

Le code MATLAB utilisé pour générer les figures est disponible ici.

Remerciements

Merci à Jean-Pierre Varnet pour la relecture. L’illustration de l’article est une image libre de droits issue de la librairie Digital Commonwealth.

Notes

1. Même si le caractère purement « observationnel » de l’étude en question est actuellement remis en cause.
2. Néanmoins, le terme de « paradoxe » est à mon avis impropre : en effet, il n’y a pas ici de violation de la logique ou des lois statistiques, mais seulement de l’intuition.
3. Voir d’autres exemples dans cette note de blog de Julia Rohrer
4. Ainsi, dans notre exemple, on aurait obtenu la même fausse corrélation en considérant la population générale mais en incluant l’hospitalisation comme facteur contrôlé dans le modèle
5. Il est également possible d’entreprendre une étude exhaustive des relations causales entre les données collectées, mais cette option est néanmoins complexe et rarement mise en œuvre en pratique[1], [2]