“– Are you interested in science, by any chance?”
The Limits of Control (Jim Jarmusch, 2009)
La notion de contrôle statistique est omniprésente dans les sciences de la vie et les sciences humaines. Chaque individu différant des autres par de très nombreux facteurs (âge, catégorie socio-professionnelle, couleur des cheveux, etc.), les scientifiques qui s’intéressent à un aspect particulier ont besoin de s’assurer que les variables non pertinentes ne parasitent pas leur mesure. C’est ici que le contrôle statistique entre en jeu : il s’agit d’un outil mathématique qui a pour objectif d’estimer l’effet propre d’une variable particulière en éliminant l’effet d’autres facteurs.
Pourtant, cet outil est très souvent mal utilisé, au point de produire des résultats erronés – voire même paradoxaux comme on le verra plus loin. Aujourd’hui, nombre de scientifiques estiment, à tort, que le moyen le plus efficace pour obtenir une estimation fiable consiste simplement à « contrôler » toutes les variables disponibles. Dans certaines branches des sciences cognitives ou de l’économétrie, on rencontre ainsi couramment des études affichant une très longue liste de facteurs intégrés pêle-mêle dans un modèle statistique : sexe, âge, niveau d’éducation, statut socio-économique, religiosité, niveau d’intérêt politique, degré de conviction idéologique, degré de conservatisme, fréquence d’exposition aux informations télévisées, taille du réseau relationnel…1 Cette tendance, que j’ai déjà évoquée au détour de ma critique du dernier ouvrage de Steven Pinker2, est si hégémonique qu’un nom lui a été attribué : « salade causale » [2] (d’autres préférant le terme de « régression-poubelle » [3]).
Voici par exemple ce que déclare le statisticien et anthropologue Richard McElreath dans le premier chapitre de son ouvrage Statistical Rethinking [2, p. 17] (ma traduction) :
L’approche qui prédomine dans de nombreuses branches de la biologie et des sciences sociales est la salade causale [qui] consiste à balancer un grand nombre de variables ‘contrôles’ dans un modèle statistique, à observer un changement de l’effet mesuré, puis à broder une histoire concernant les relations de causalité entre ces variables. La salade causale semble fondée sur l’idée que seule une omission de variables contrôles risque de conduire à des conclusions erronées. Mais l’inclusion de certaines variables peut tout autant induire en erreur.
Ce constat sans appel est partagé par plusieurs statisticiens et statisticiennes de premier plan, notamment Judea Pearl3, Christopher Achen4, ou Julia Rohrer5: une vaste majorité des études observationnelles souscrivent au pseudo-théorème « plus le nombre de variables contrôlées est grand, meilleure est l’estimation ». Ceci est peut-être en partie lié au terme même de « contrôle » qui évoque une impression de précision et de fiabilité – le but des scientifiques n’est-il pas justement de contrôler au maximum la mesure des effets étudiés ? La plupart des personnes qui utilisent les statistiques n’étant elles-mêmes pas des statisticiens et statisticiennes aguerries, ce nom ambigu peut les conduire à surestimer le potentiel de l’outil et à fausser l’interprétation de son fonctionnement.6
Dans le paragraphe suivant, j’illustrerai le principe du contrôle statistique au moyen de données factices très simples, avant de mettre en évidence les potentiels effets dévastateurs de son mésusage.
Qu’est-ce que le contrôle statistique ? Un exemple factice.
Imaginons que nous souhaitions évaluer si le vieillissement exerce une influence sur la joie de vivre, une question abondamment débattue en économétrie. Une approche empirique assez intuitive de cette question consisterait à sélectionner aléatoirement un large panel de participants et de participantes, de noter leur âge et de leur demander d’évaluer subjectivement leur joie de vivre sur une échelle de 1 à 3 : ‘De manière générale, diriez-vous que vous êtes : 1 – Pas très heureux ; 2 – Assez heureux ; 3 – Très heureux ?’. C’est, par exemple, ce qu’ont entrepris les économistes David Blanchflower et Andrew Oswald, en agrégeant les réponses de 500 000 personnes vivant en Europe ou aux États-Unis [7].
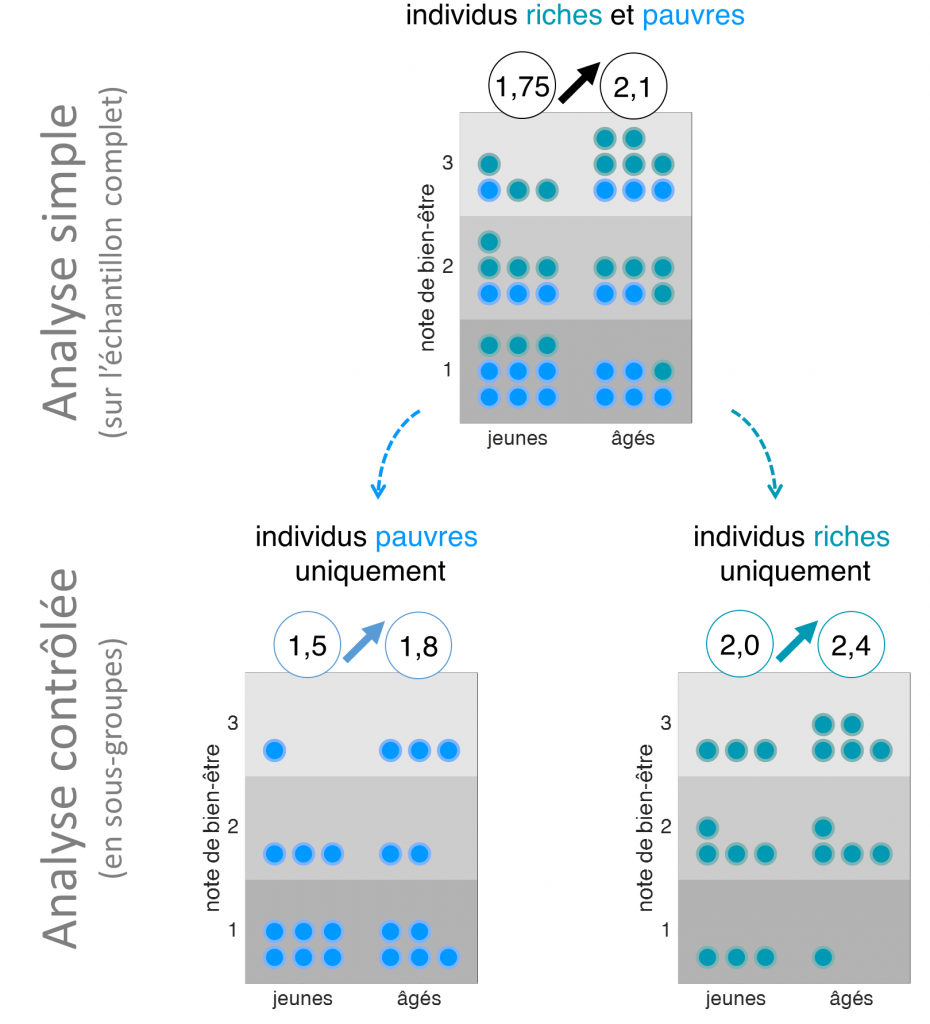
Une fois les réponses collectées, nous pouvons ensuite mesurer la différence entre les « notes de bien-être » de plusieurs groupes d’âges, et tenter d’interpréter ce résultat. Sur les données étatsuniennes, cette analyse indique que les personnes sondées les plus âgées se déclarent en moyenne plus heureuses. J’ai représenté la situation de façon schématique sur la figure 1 (ligne du haut) sur un échantillon imaginaire réduit à 20 individus jeunes et 20 individus âgés : la note moyenne de bien-être est de 1,75/3 pour les plus jeunes, contre 2,1/3 pour les plus âgés.
Outre les difficultés inhérentes à l’interprétation de cette observation7, un problème d’ordre statistique se pose. Notre échantillon aléatoire de population comporte des personnes possédant des revenus plus ou moins élevés, et les individus les plus jeunes ont, en moyenne, de plus faibles revenus. Dès lors, comment être certain que la différence observée est véritablement liée à l’âge, et non une conséquence de la différence de revenus entre les plus jeunes et les plus âgés – en supposant que les personnes plus riches sont plus susceptibles de se déclarer heureuses ? Ceci conduirait indubitablement à une lecture très différente du même ensemble de données.
Pour résoudre ce problème, on fait appel au contrôle statistique. Ici, l’application de cet outil est relativement simple. Elle consiste, en essence, à réaliser cette même du lien entre âge et joie de vivre séparément, chez les individus les plus riches, puis chez les individus les plus pauvres, et à vérifier que des résultats concordants sont observés quel que soit le niveau de revenus. Notons que, les revenus étant désormais relativement homogènes au sein de chaque sous-groupe, nous pouvons être confiants que le lien observé entre âge et joie de vivre n’est pas une conséquence indirecte de l’amélioration des conditions financières au cours de la vie. Cette façon, assez intuitive, de mesurer la relation entre deux variables d’intérêt (ici, l’âge et le bien-être déclaré) en éliminant l’effet potentiel d’un troisième facteur (le niveau de revenu) constitue le cœur du principe du contrôle statistique. La partie inférieure de la figure 1 illustre ce procédé sur notre échantillon factice : dans le sous-groupe le plus pauvre comme dans le sous-groupe le plus riche, la note moyenne de joie de vivre est plus élevée chez les individus âgés que chez les individus les plus jeunes.8
Il convient d’ouvrir ici une parenthèse pour souligner que la définition des groupes « jeune » vs. « âgé », ou « hauts revenus » vs. « bas revenus » est assez arbitraire. Il s’agit en fait d’un choix purement didactique : en pratique, le contrôle statistique, implémenté au moyen d’une régression multiple, se généralise aisément aux variables continues. Notons également que rien n’empêche de contrôler plusieurs variables en même temps – ce qui reviendrait ici à considérer des sous-sous-groupes. Comme je l’ai mentionné en introduction, il n’est pas rare de voir certaines études contrôlant pour un grand nombre de variables : ainsi dans leur étude sur vieillissement et bien-être, Blanchflower et Oswald contrôlent simultanément l’éducation, la race, la catégorie de travail, la présence d’enfants à charge, le divorce des parents, l’année de naissance, et le statut marital. Intéressons-nous maintenant à cette dernière variable.
Un paradoxe statistique : contrôler pour le statut matrimonial
De même que nous avons utilisé précédemment le contrôle statistique pour nous assurer que l’effet de l’âge sur le bien-être déclaré n’était pas une conséquence indirecte de l’augmentation du niveau de revenus, on peut à présent se demander s’il n’est pas une conséquence indirecte du mariage. Il est en effet envisageable qu’un lien existe entre mariage et joie de vivre (par exemple : les personnes se déclarant plus heureuses ont plus tendance à se marier et à rester mariées) et on pourrait donc souhaiter contrôler la variable « statut matrimonial » (simplifiée ici en marié vs. célibataire).
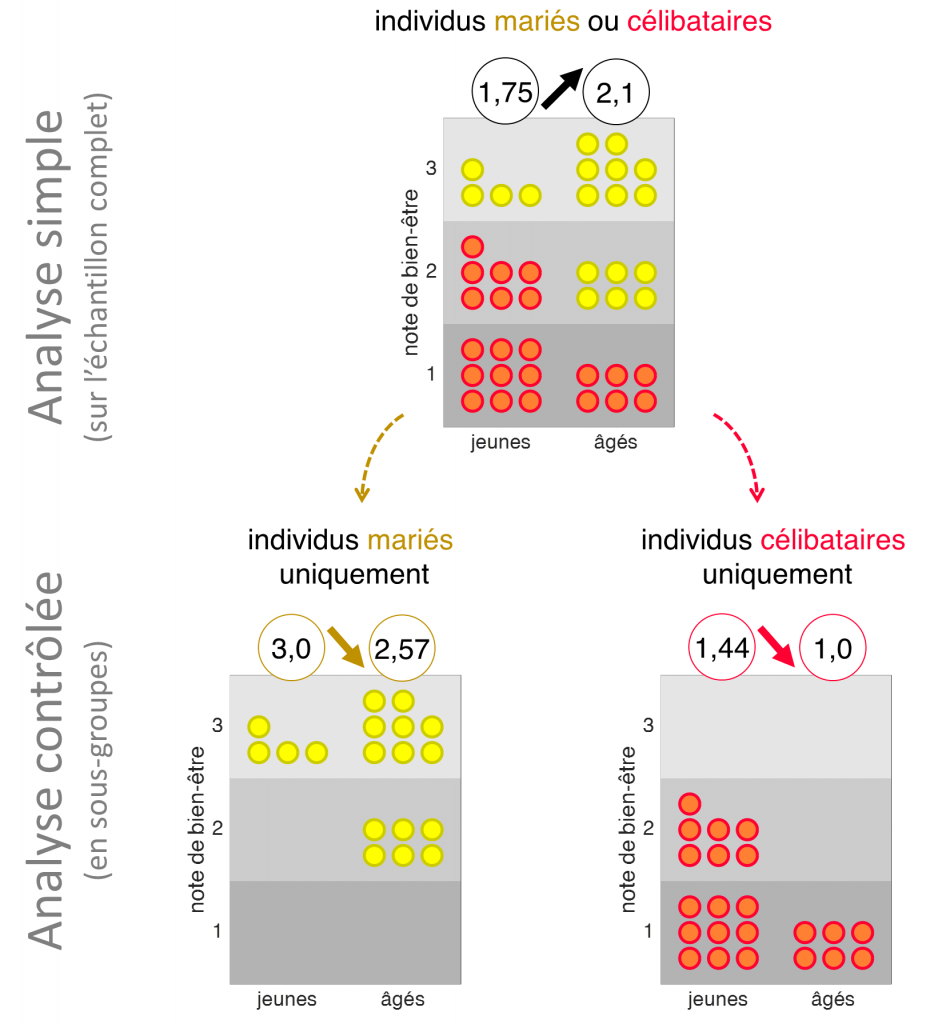
Imaginons, pour les besoins de notre exemple, que le mariage soit très fortement lié aux deux variables, âge et bonheur, qui nous intéressent : en forçant le trait, on supposera que ne sont mariées au moment du sondage que les personnes âgées et/ou d’un niveau de bien-être subjectif relativement élevé (les points jaunes sur la figure 2). Bien évidemment, l’analyse simple, menée sur l’ensemble de l’échantillon toutes conditions matrimoniales confondues, donne exactement les mêmes résultats que précédemment. En revanche, un résultat paradoxal apparaît lorsqu’on réitère l’analyse en contrôlant cette fois pour le statut matrimonial, c’est-à-dire en dissociant les groupes « mariés » et « célibataires ». Alors que, à l’échelle de l’échantillon complet, la note moyenne de bien-être est plus élevée chez les individus âgés que chez les individus les plus jeunes, on observe la tendance inverse au sein de chacun des deux sous-groupes : les personnes âgées semblent en moyenne moins heureuses que les jeunes.
Que faut-il en conclure ? Que la joie de vivre déclinerait en fait avec l’âge, une fois pris en compte l’effet du mariage ? Eh bien non. Le résultat obtenu par cette analyse contrôlée ne reflète pas la possible relation causale entre âge et bien-être, mais uniquement le lien que ces deux variables entretiennent avec le mariage.
En réalité, on peut envisager chacune des deux sous-analyses représentées dans la partie inférieure de la figure 2 comme un paradoxe de Berkson (un phénomène que j’ai décrit dans un précédent billet) : l’inclusion des individus dans chacun des deux sous-groupes est biaisé car il dépend directement des deux variables qui nous intéressent, introduisant ainsi une relation robuste mais trompeuse entre ces dernières. Ce que traduit cette corrélation négative c’est que, si nous savons qu’une personne est mariée ou non, il est possible de relier son âge et son bien-être – ce qui n’a rien d’étonnant puisque dans notre exemple factice nous avons justement supposé, de façon caricaturale, que le mariage dépendait uniquement de l’âge et du bien-être des individus. Autrement dit, dans ce cas de figure, l’analyse contrôle conduit à biaiser notre estimation en y incorporant l’effet indirect d’un troisième facteur, l’exact opposé du but recherché.
Plus intuitivement, s’il semblait assez légitime dans le cas du niveau de revenu de s’assurer que notre analyse simple sur l’échantillon complet se vérifie chez les individus riches comme chez les individus pauvres, dans le cas de la variable mariage, ceci nous conduit à une forme de raisonnement circulaire consistant à mesurer la relation entre âge et bien-être sur deux sous-groupes définis… par une relation entre âge et bien-être. C’est ce qui différencie notre cas valide d’application du contrôle statistique (le niveau de revenu, qui dépend certes de l’âge, mais pas a priori de la combinaison de l’âge et du niveau de bien-être) et le cas erroné (le statut marital, dépendant conjointement des deux variables, ce qu’on appelle en statistiques un « collisionneur »).
Pour revenir à l’étude de Blanchflower et Oswald, les conclusions des auteurs concernant l’influence du vieillissement sur la joie de vivre furent remises en cause du fait de l’inclusion du statut matrimonial comme variable contrôle [8] et ce problème est même désormais présenté comme un cas d’école dans les manuels de statistiques [2, p. 182].
Du bon usage du contrôle statistique
Dans l’exemple factice précédent, nous avons vu que le contrôle statistique peut s’avérer utile pour éliminer l’influence d’un facteur non pertinent lors de la mesure d’un effet statistique entre deux variables, mais qu’il achoppe si on l’applique par inadvertance à un collisionneur, c’est-à-dire un facteur qui dépend conjointement des deux variables d’intérêt. Notez que j’ai choisi d’illustrer ici le potentiel dévastateur d’une telle erreur à l’aide d’un paradoxe statistique mais, selon le lien que les collisionneurs entretiennent avec les variables d’intérêt, ils peuvent également avoir pour résultat d’amplifier la corrélation étudiée, ce qui est tout aussi problématique, ou de ne pas l’affecter du tout. En outre, je n’ai décrit ici qu’un seul exemple de situation aboutissant à une utilisation erronée du contrôle statistique, on pourra se reporter aux livres de Richard McElreath [2] ou de Judea Pearl [4] pour une liste plus exhaustive9.
Face à ces difficultés, on comprend aisément la confusion qui règne actuellement au sein de la communauté scientifique quant à l’emploi des variables contrôle (cf. notes 3, 4, et 5), et il pourrait être tentant à ce stade de sombrer dans le défaitisme. Cependant, il n’est pas question ici de rejeter en bloc le contrôle statistique. Celui-ci peut s’avérer un instrument très puissant lorsqu’il est employé avec discernement. Le problème réside essentiellement dans l’incertitude quant aux variables à considérer dans l’analyse. Pour tenter d’endiguer la prolifération des études fondées sur l’inclusion aveugle d’un maximum de contrôles, les statisticiens et statisticiennes de l’inférence causale ont proposé une approche méthodique permettant d’identifier les collisionneurs potentiels.
Leur constat de départ est le suivant : les données seules ne sont pas suffisantes pour résoudre le problème, c’est-à-dire pour déterminer si une variable que nous souhaitons contrôler est, ou non, un collisionneur. Dans nos deux exemples, rien ne différencie a priori le niveau de revenu et le statut matrimonial d’un point de vue purement statistique. Pour déterminer que le seconde est un collisionneur mais non le premier, nous avons besoin de faire appel à un autre type de connaissance sur nos variables : les relations de causalité qui les relient (le niveau de revenu dépend de l’âge et peut affecter le bien-être ; le statut marital dépend simultanément du bien-être et de l’âge). La résolution de notre problème requiert donc un modèle causal, qui est complémentaire du modèle statistique.
La marche à suivre préconisée par l’analyse causale est donc la suivante :
1) En premier lieu, tracer le réseau de relations causales postulé entre les variables considérées. On obtient ainsi un diagramme causal comme celui décrit dans ce précédent billet.
2) Dans un second temps, l’analyse de ce réseau au moyen d’un ensemble de règles simples permet de démêler les collisionneurs des contrôles potentiels et ainsi de déterminer quelle variable ou ensemble de variables doivent être contrôlés pour obtenir une estimation fiable.
Cette approche offre ainsi un moyen de s’extirper de la salade causale. Mais elle représente surtout une révolution dans la façon d’envisager les statistiques. En opposition avec l’automatisation du traitement de grand jeux de données qui prévaut actuellement, l’analyse causale affirme que toute conclusion statistique est assujettie à un ensemble d’hypothèse sur les relations causales entre les variables – hypothèses qui ne peuvent être formulées que par un humain ayant des connaissances extérieures sur la signification de ces variables et les relations qui les lient. Certaines de ces hypothèses peuvent être consensuelles (il est évident que le niveau de revenu peut dépendre de l’âge mais non l’inverse) ou non (nous avons supposé que les personnes plus riches étaient plus susceptibles de se déclarer heureuses, mais nous avons omis l’éventualité que la richesse dépende également en partie du bien-être), mais elles ne peuvent être entièrement déduites des données elles-mêmes10. Cette façon de repenser les statistiques est passionnante et j’espère avoir l’occasion de l’approfondir dans un prochain billet.
En attendant, reste que des milliers d’études observationnelles sont publiées chaque année dans des revues scientifiques internationales malgré une méthodologie statistique bancale, et servent parfois à valider des politiques publiques, des discours sur le développement humain, ou encore des théories économiques. Il est très difficile d’évaluer l’impact de l’utilisation abusive du contrôle statistique sur ces résultats, et la vérification méticuleuse de leurs conclusions va représenter une entreprise colossale. Pour l’heure, comme le conclut Christopher Achen [3, p. 17], nous devons cesser de prendre pour argent comptant les travaux empiriques impliquant l’inclusion sans discernement d’un nombre élevé de contrôles. Et nous devons cesser de commettre cette erreur.
Remerciements
Image d’illustration : Isaach de Bankolé et Yūki Kudō dans The Limits of Control (Jim Jarmush, 2009).
Références
[1] J. Matthes, « Do Hostile Opinion Environments Harm Political Participation? The Moderating Role of Generalized Social Trust », Int J Public Opin Res, vol. 25, no 1, p. 23‑42, mars 2013, doi: 10.1093/ijpor/eds006.
[2] R. McElreath, Statistical Rethinking : A Bayesian Course with R Examples. Boca Raton, UNITED STATES: Chapman and Hall/CRC, 2015. [En ligne]. Disponible sur: http://ebookcentral.proquest.com/lib/ucl/detail.action?docID=4648054
[3] C. H. Achen, « Let’s Put Garbage-Can Regressions and Garbage-Can Probits Where They Belong », Conflict Management and Peace Science, vol. 22, no 4, p. 327‑339, déc. 2005, doi: 10.1080/07388940500339167.
[4] J. Pearl et D. Mackenzie, The Book of Why: The New Science of Cause and Effect. Penguin UK, 2018.
[5] J. M. Rohrer, « Thinking Clearly About Correlations and Causation: Graphical Causal Models for Observational Data », Advances in Methods and Practices in Psychological Science, vol. 1, no 1, p. 27‑42, mars 2018, doi: 10.1177/2515245917745629.
[6] P. E. Spector et M. T. Brannick, « Methodological Urban Legends: The Misuse of Statistical Control Variables », Organizational Research Methods, vol. 14, no 2, p. 287‑305, avr. 2011, doi: 10.1177/1094428110369842.
[7] D. G. Blanchflower et A. J. Oswald, « Is well-being U-shaped over the life cycle? », Social Science & Medicine, vol. 66, no 8, p. 1733‑1749, avr. 2008, doi: 10.1016/j.socscimed.2008.01.030.
[8] N. Glenn, « Is the apparent U-shape of well-being over the life course a result of inappropriate use of control variables? A commentary on Blanchflower and Oswald (66: 8, 2008, 1733–1749) », Social Science & Medicine, vol. 69, no 4, p. 481‑485, août 2009, doi: 10.1016/j.socscimed.2009.05.038.
Le code MATLAB correspondant à l’analyse de l’exemple factice est disponible ici.
Notes
- Ces exemples de variables contrôles sont issus d’une étude sur l’effet de l’environnement social sur le niveau de participation politique. [1]
- Celui-ci y affirme notamment que ‘Les études qui évaluent l’éducation […] et la richesse […], en gardant constants tous les autres paramètres, suggèrent que le fait d’investir dans l’éducation enrichit réellement le pays’ (c’est moi qui souligne), ce qui est un parfait exemple d’une compréhension erronée — mais très répandue — de la notion de contrôle statistique.
- “Oddly, statisticians both over- and underrate the importance of adjusting for possible confounders. They overrate it in the sense that they often control for many more variables than they need to and even for variables that they should not control for. I recently came across a quote from a political blogger named Ezra Klein who expresses this phenomenon of “overcontrolling” very clearly:
“You see it all the time in studies. ‘We controlled for…’ And then the list starts. The longer the better. Income. Age. Race. Religion. Height. Hair color. Sexual preference. Crossfit attendance. Love of parents. Coke or Pepsi. The more things you can control for, the stronger your study is—or, at least, the stronger your study seems. Controls give the feeling of specificity, of precision.… But sometimes, you can control for too much. Sometimes you end up controlling for the thing you’re trying to measure.”
Klein raises a valid concern. Statisticians have been immensely confused about what variables should and should not be controlled for, so the default practice has been to control for everything one can measure. The vast majority of studies conducted in this day and age subscribe to this practice. It is a convenient, simple procedure to follow, but it is both wasteful and ridden with errors.” [4] - “Many social scientists believe that dumping long lists of explanatory variables into linear regression, probit, logit, and other statistical equations will successfully “control” for the effects of auxiliary factors. Encouraged by convenient software and ever more powerful computing, researchers also believe that this conventional approach gives the true explanatory variables the best chance to emerge. The present paper argues that these beliefs are false, and that statistical models with more than a few independent variables are likely to be inaccurate.” [3]
- “Many researchers have tried to bridge the gap between observational data and (more or less explicit) causal conclusions by statistically controlling for third variables. Alas, such attempts often lack proper justification: The choice of control variables is determined by norms in the domain and by the variables available in the data set. Often, the analysis follows the rationale that “more control” is always better than less. Models resulting from such an approach have been labeled “garbage-can regression” because the idea that the inclusion of a multitude of control variables will necessarily improve (and will not worsen) causal inference is a methodological urban legend at best.” [5]
- Ce phénomène est bien sûr aggravé par la baisse des dotations des laboratoires de recherche, qui ne leur permettent bien souvent plus d’embaucher d’ingénieur·e·s en statistiques, et à l’endogamie du processus de revue par les pairs qui conduit à une écrasante majorité d’articles publiés sans avoir été jamais corrigés par un ou une statisticienne.
- Par exemple : la notion de joie de vivre est-elle la même pour tous les participants ? Est-elle culturellement située ? Ce protocole basé sur l’introspection ne risque-t-il pas d’introduire un biais en fonction de l’âge des personnes testées ?
- Plus précisément, la mesure de l’effet de l’âge sur le bien être en contrôlant pour le niveau de revenu correspond ici à la moyenne des effets mesurés dans les deux sous-groupes, soit (1,8 – 1,5 + 2,4 – 2,0) / 2 = 0,35.
- Même lorsque les variables contrôle sont choisies avec soin, d’autres problèmes peuvent conduire notre analyse statistique à des conclusions erronées. David Louapre évoque notamment dans un récent billet les conséquences potentiellement désastreuses de la présence d’une erreur de mesure dans nos variables.
- Il est néanmoins possible d’éliminer certaines hypothèses causales sur la base des données.